Finite State Automaton Challenges
Automaton is a machine that answers a specific question without human intervention once it is turned on, such as: Whether a + b = c?
In this game, we will use the simplest automaton model, the Finite State Automaton, to cope with 70 challenges. They come from character string manipulation, binary numbers, and daily life. Don't worry if you are unfamiliar with Finite State Automaton; this game contains a tutorial to get started quickly. Also, you can read the following introduction.Finite State Automaton
Finite State Automaton (FSA) is the simplest automaton type. A finite state automaton consists of several states and transition rules. A transition rule describes when a state transits to another. So, it looks like a metro map. The clients of a finite state automaton are the character strings. It decides which strings are accepted and which strings are rejected. For example, an FSA can accept valid emails, phone numbers, etc. Now, let's dive into the first example:
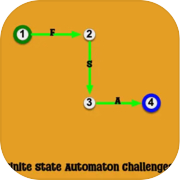
It has two states: the left state "1," and the right state "2". "1" marked with the green color means the automaton starts here. "2" marked with the blue color means that the automaton accepts the input string only if it stops here and read all characters in the order of the string. Consequently, this automaton is to accept "a" and reject any other string.
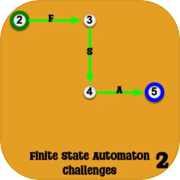
Question: try to design an FSA accepting "ab" and an FSA accepting "a" or "b" (abbr., "a|b") on your own (They are two challenges in the game).Finite State Automaton with Various StatesTraditional finite state automata have only three types of states: begin, accept, and normal. In this game, you can play automata with different states at different levels. The picture below shows an example.
Non-deterministicThe most essential concept of FSA (and other automaton types) is called Non-deterministic. To introduce this concept, here is the second example of an automaton. It accepts all strings (only consisting of 'a' and 'b') ending with 'b':
Run this automaton over "b" in your head: (1) It starts at "1", runs the self-loop of "1", then reads all of "b" as well as stops at "1", so reject "b"; (2) It starts at "1" and transits to "2", then reads all of "b" as well as stops at "2", so accept "b". A non-deterministic finite state automaton (NFA) accepts a string if at least one trace ends at a state marked with the blue color.
Run this automaton over "ab" in your head: (1) It starts at "1", runs the self-loop of "1" twice, then reads all of "ab" as well as stops at "1", so reject "ab"; (2) It starts at "1", run the self-loop of "1" once, and transits to "2", then reads all of "b" as well as stops at "2", so accept "ab."
Non-deterministic is essential because it allows the FSA to guess, which lets us design an automaton naturally (since we, human beings, like to guess) and quickly.
In this game, we will use the simplest automaton model, the Finite State Automaton, to cope with 70 challenges. They come from character string manipulation, binary numbers, and daily life. Don't worry if you are unfamiliar with Finite State Automaton; this game contains a tutorial to get started quickly. Also, you can read the following introduction.Finite State Automaton
Finite State Automaton (FSA) is the simplest automaton type. A finite state automaton consists of several states and transition rules. A transition rule describes when a state transits to another. So, it looks like a metro map. The clients of a finite state automaton are the character strings. It decides which strings are accepted and which strings are rejected. For example, an FSA can accept valid emails, phone numbers, etc. Now, let's dive into the first example:
It has two states: the left state "1," and the right state "2". "1" marked with the green color means the automaton starts here. "2" marked with the blue color means that the automaton accepts the input string only if it stops here and read all characters in the order of the string. Consequently, this automaton is to accept "a" and reject any other string.
Question: try to design an FSA accepting "ab" and an FSA accepting "a" or "b" (abbr., "a|b") on your own (They are two challenges in the game).Finite State Automaton with Various StatesTraditional finite state automata have only three types of states: begin, accept, and normal. In this game, you can play automata with different states at different levels. The picture below shows an example.
Non-deterministicThe most essential concept of FSA (and other automaton types) is called Non-deterministic. To introduce this concept, here is the second example of an automaton. It accepts all strings (only consisting of 'a' and 'b') ending with 'b':
Run this automaton over "b" in your head: (1) It starts at "1", runs the self-loop of "1", then reads all of "b" as well as stops at "1", so reject "b"; (2) It starts at "1" and transits to "2", then reads all of "b" as well as stops at "2", so accept "b". A non-deterministic finite state automaton (NFA) accepts a string if at least one trace ends at a state marked with the blue color.
Run this automaton over "ab" in your head: (1) It starts at "1", runs the self-loop of "1" twice, then reads all of "ab" as well as stops at "1", so reject "ab"; (2) It starts at "1", run the self-loop of "1" once, and transits to "2", then reads all of "b" as well as stops at "2", so accept "ab."
Non-deterministic is essential because it allows the FSA to guess, which lets us design an automaton naturally (since we, human beings, like to guess) and quickly.
Available on devices:
- Windows